Stacking made easy with Sklearn

The underlying principle of ensemble methods is that there is a strength to be found in unity. By combining multiple methods, each with its own pros and cons, more powerful models can be created.

The Whole is Greater than the Sum of its Parts — Aristotle

This quote especially rings true when it concerns stacking, a method for combining many different learners into a more powerful model.

The main reason for writing this article is not to explain how stacking works, but to demonstrate how you can use Scikit-Learn V0.22 in order to simplify stacking pipelines and create interesting models.

1. Stacking

Although there are many great sources that introduce stacking (here, here, and here), let me quickly get you up to speed.

Stacking is a technique that takes several regression or classification models and uses their output as the input for the meta-classifier/regressor.

In its essence, stacking is an ensemble learning technique much like Random Forests where the quality of prediction is improved by combining, typically, weak models.

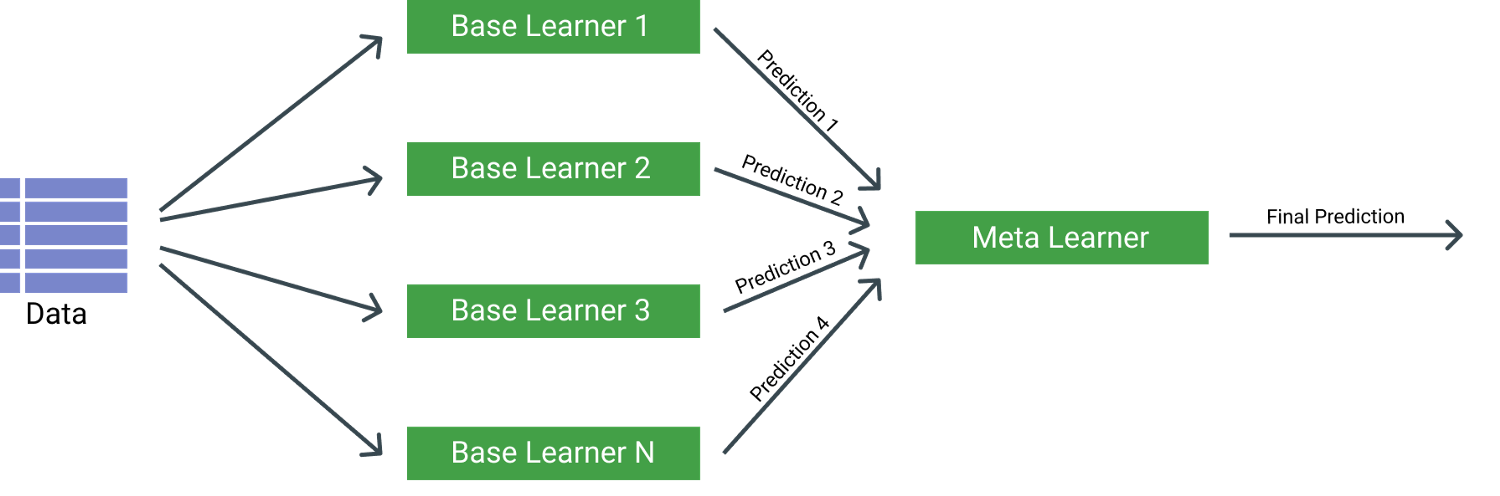
Overview of a single level Stacking model.

The image above gives a basic overview of the principle of stacking. It typically consists of many weak base learnings or several stronger. The meta learner then learns based on the prediction outputs of each base learner.

2. Sklearn Stacking

Although there are many packages that can be used for stacking like mlxtend and vecstack, this article will go into the newly added stacking regressors and classifiers in the new release of scikit-learn.

First, we need to make sure to upgrade Scikit-learn to version 0.22:

pip install --upgrade scikit-learn

The first model that we are going to make is a classifier that can predict the specifies of flowers. The model is relatively simple, we use a Random Forest and k-Nearest Neighbors as our base learners and a Logistic Regression as our meta learner.

Coding stacking models can be quite tricky as you will have to take into account the folds that you want to generate and cross-validation at different steps. Fortunately, the new scikit-learn version makes it possible to create the model shown above in just a few lines of code:

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier, StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

X, y = load_iris(return_X_y=True)

# Create Base Learners
base_learners = [
                 ('rf_1', RandomForestClassifier(n_estimators=10, random_state=42)),
                 ('rf_2', KNeighborsClassifier(n_neighbors=5))             
                ]

# Initialize Stacking Classifier with the Meta Learner
clf = StackingClassifier(estimators=base_learners, final_estimator=LogisticRegression())

# Extract score
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
clf.fit(X_train, y_train).score(X_test, y_test)

And that is basically it! A stacking classifier in only a few lines of code.

3. Cross-Validation

One difficulty with stacking is where you choose to apply cross-validation. We could apply it solely at the meta learner level, but that would likely result in overfitting our model since the outputs of the base learners could have been overfitted.

Although there are many strategies for approaching this problem, in scikit-learn stacking was implemented as follows:

Base learners are fitted on the full X while the final estimator is trained using cross-validated predictions of the base learners using cross_val_predict.

This means that the predictions of each individual base learner are stacked together and used as input to a meta learner to compute the prediction. This meta learner is then trained through cross-validation.

Cross-validation is automatically set to 5-fold CV but can be adjusted manually:


clf = StackingClassifier(estimators=base_learners,
                         final_estimator=LogisticRegression(),  
                         cv=10)

But that’s not all, you can also put in any cross-validation strategy you want:

from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
clf = StackingClassifier(estimators=base_learners, final_estimator=LogisticRegression(), cv=loo)

4. Multi-layer Stacking

In step 2 we have created a StackingClassifier with a single layer of base learners. But what if you want to replace the meta learner by another set of base learners? How would you add layers to increase the complexity of the model?

Here, we will add another layer of learners to the model in step 2 in order to get an understanding of how to code that solution.

In the image above, we can see that we want to add a layer that includes two additional classifiers, namely a Decision Tree and a Random Forest.

In order to do that, we create two lists of estimators, one for each layer. We create a StackingClassifier using the second layer of estimators with the final model, namely the Logistic Regression. Then, we create a new StackingClassifier with the first layer of estimators to create the full pipeline of models.


from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier, StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier

X, y = load_iris(return_X_y=True)

# Create Learners per layer
layer_one_estimators = [
                        ('rf_1', RandomForestClassifier(n_estimators=10, random_state=42)),
                        ('knn_1', KNeighborsClassifier(n_neighbors=5))             
                       ]
layer_two_estimators = [
                        ('dt_2', DecisionTreeClassifier()),
                        ('rf_2', RandomForestClassifier(n_estimators=50, random_state=42)),
                       ]
layer_two = StackingClassifier(estimators=layer_two_estimators, final_estimator=LogisticRegression())

# Create Final model by 
clf = StackingClassifier(estimators=layer_one_estimators, final_estimator=layer_two)

X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=42)
clf.fit(X_train, y_train).score(X_test, y_test)

As you can see the complexity of the model increases rapidly with each layer. Moreover, without proper cross-validation, you can easily overfit the data using these many layers.

Conclusion

Stacking can be a tricky subject as it requires a significant understanding of data leakage in order to select the correct procedure. Make sure to always do extensive validation of your models in order to understand its generalizability.

If you are, like me, passionate about AI, Data Science or Psychology, please feel free to add me on LinkedIn.