Skip to content

BERTopic: What Is So Special About v0.16?

Open In Colab

My ambition for BERTopic is to make it the one-stop shop for topic modeling by allowing for significant flexibility and modularity.

That has been the goal for the last few years and with the release of v0.16, I believe we are a BIG step closer to achieving that.

First, let’s take a small step back. What is BERTopic?

Well, BERTopic is a topic modeling framework that allows users to essentially create their version of a topic model. With many variations of topic modeling implemented, the idea is that it should support almost any use case.o

The modular nature of BERTopic allows you to build your topic model however you want. Switching components allows BERTopic to grow with the latest developments in Language AI.

With v0.16, several features were implemented that I believe will take BERTopic to the next level, namely:

  • Zero-Shot Topic Modeling

  • Model Merging

  • More Large Language Model (LLM) Support

Just a few of BERTopic’s capabilities.

In this tutorial, we will go through what these features are and for which use cases they could be helpful.

To start with, you can install BERTopic (with HF datasets) as follows:

pip install bertopic datasets

You can also follow along with the Google Colab Notebook to make sure everything works as intended.

UPDATE: I uploaded a video version to YouTube that goes more in-depth into how to use these new features:

Zero-Shot Topic Modeling: A Flexible Technique

Zero-shot techniques generally refer to having no examples to train your data on. Although you know the target, it is not assigned to your data.

In BERTopic, we use Zero-shot Topic Modeling to find pre-defined topics in large amounts of documents.

Imagine you have ArXiv abstracts about Machine Learning and you know that the topic “Large Language Models” is in there. With Zero-shot Topic Modeling, you can ask BERTopic to find all documents related to “Large Language Models”.

In essence, it is nothing more than semantic search! But… there is a neat trick ;-)

When you try to find those documents related to “Large Language Models”, there will be many left not about those topics. So, what do you do with those topics? You use BERTopic to find all topics that were left!

As a result, you will have three scenarios of Zero-shot Topic Modeling:

  • No zero-shot topics were detected. This means that none of the documents would fit with the predefined topics and a regular BERTopic would be run.

  • Only zero-shot topics were detected. Here, we would not need to find additional topics since all original documents were assigned to one of the predefined topics.

  • Both zero-shot topics and clustered topics were detected. This means that some documents would fit with the predefined topics whereas others would not. For the latter, new topics were found.

Using Zero-shot BERTopic is straightforward:

from datasets import load_dataset

from bertopic import BERTopic
from bertopic.representation import KeyBERTInspired

# We select a subsample of 5000 abstracts from ArXiv
dataset = load_dataset("CShorten/ML-ArXiv-Papers")["train"]
docs = dataset["abstract"][:5_000]

# We define a number of topics that we know are in the documents
zeroshot_topic_list = ["Clustering", "Topic Modeling", "Large Language Models"]

# We fit our model using the zero-shot topics
# and we define a minimum similarity. For each document,
# if the similarity does not exceed that value, it will be used
# for clustering instead.
topic_model = BERTopic(
    embedding_model="thenlper/gte-small", 
    min_topic_size=15,
    zeroshot_topic_list=zeroshot_topic_list,
    zeroshot_min_similarity=.85,
    representation_model=KeyBERTInspired()
)
topics, probs = topic_model.fit_transform(docs)

We can view the three pre-defined topics along with several newly discovered topics:

topic_model.get_topic_info()

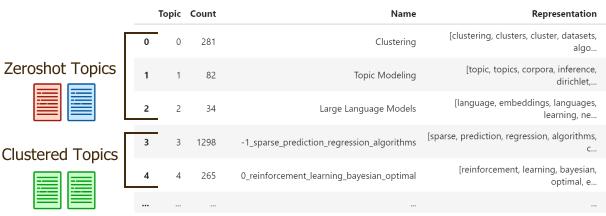
Note that although we have pre-defined names for the topics, we allow BERTopic for additional representations.

This gives exciting new insight into pre-defined topics!

So… when do you use Zero-shot Topic Modeling?

If you already know some of the topics in your data, this is a great solution for finding them! Since it can discover both pre-defined and new topics, is an incredibly flexible technique.

Model Merging: Federated and Incremental Learning

This is a fun new feature, model merging!

Model merging refers to BERTopic’s capability to combine multiple pre-trained BERTopic models to create one large topic model. It explores which topics should be merged and which should remain separate.

It works as follows. When we pass a list of models to this new feature, .merge_models, the first model in the list is chosen as the baseline. This baseline is used to check whether all other models contain new topics based on the similarity between their topic embeddings.

Dissimilar topics are added to the baseline model whereas similar topics are assigned to the topic of the baseline. This means that we need the embedding models to be the same.

When merging BERTopic models, duplicate topics will be merged and all other topics will be kept the same.

Merging pre-trained BERTopic models is straightforward and only requires a few lines of code:

from bertopic import BERTopic

# Merge 3 pre-trained BERTopic models
merged_model = BERTopic.merge_models(
    [topic_model_1, topic_model_2, topic_model_3]
)

And that is it! With a single function, .merge_models, you can merge pre-trained BERTopic models.

The benefit of merging pre-trained models is that it allows for a variety of creative and useful use cases. For instance, we could use it for:

  • Incremental Learning — We can continuously discover new topics by iteratively merging models. This can be used for issue tickets to quickly uncover pressing bugs/issues.

  • Batched Learning — Compute and memory problems can arise with large datasets or when you simply do not have the hardware for it. By splitting the training process up into smaller models, we can get similar performance whilst reducing the necessary compute.

  • Federated Learning — Merging models allow for the training to be distributed among different clients who do not wish to share their data. This increases privacy and security with respect to their data especially if a non-keyword-based method is used for generating the representations, such as using a Large Language Model.

Federated Learning is rather straightforward, simply run .merge_models on your central server.

The other two, incremental and batched learning, might require a bit of an example!

Incremental and Batched Learning

To perform both incremental and batched learning, we are going to mimic a typical .partial_fit pipeline. Here, we will train a base model first and then iteratively add a small newly trained model.

In each iteration, we can check any topics that were added to the base model:

from bertopic import BERTopic
from bertopic.representation import KeyBERTInspired
from datasets import load_dataset

# Prepare documents
all_docs = load_dataset("CShorten/ML-ArXiv-Papers")["train"]["abstract"][:20_000]
doc_chunks = [all_docs[i:i+5000] for i in range(0, len(all_docs), 5000)]

# Base Model
representation_model = KeyBERTInspired()
base_model = BERTopic(representation_model=representation_model, min_topic_size=15).fit(doc_chunks[0])

# Iteratively add small and newly trained models
for docs in doc_chunks[1:]:
    new_model = BERTopic(representation_model=representation_model, min_topic_size=15).fit(docs)
    updated_model = BERTopic.merge_models([base_model, new_model])

    # Let's print the newly discover topics
    nr_new_topics = len(set(updated_model.topics_)) - len(set(base_model.topics_))
    new_topics = list(updated_model.topic_labels_.values())[-nr_new_topics:]
    print("The following topics are newly found:")
    print(f"{new_topics}\n")

    # Update the base model
    base_model = updated_model

To illustrate, this will give back newly found topics such as:

>  The following topics are newly found:
[
 ‘50_forecasting_predicting_prediction_stocks’, 
 ‘51_activity_activities_accelerometer_accelerometers’, 
 ‘57_rnns_deepcare_neural_imputation’
]

It retains everything from the original model, including

Not only do we reduce the compute by splitting the training up into chunks, but we can monitor any new topics that were added to the model.

In practice, you can train a new model with a frequency that fits your use case. You might check for new topics monthly, weekly, or even daily if you have enough data.

More Large Language Model Support

Although we could use Large Language Models (LLMs) for a while now in BERTopic, the v0.16 release has several smaller additions that make working with LLMs a nicer experience!

To sum up, the following were added:

Let’s explore a short example of the first two features, llama.cpp and document truncation.

When you pass documents to any LLM module, they might exceed its token limit. Instead, we can truncate the documents passed to the LLM by defining a tokenizer and a doc_length.

The different methods for tokenization when truncating documents.

The definition of a doc_length depends on the tokenizer you use. For example, a value of 100 can refer to truncating by the number of tokens or even characters.

Before documents are added to the prompt, they can be truncated first based on the tokenization strategy.

To use this together with llama-cpp-python , let’s consider the following example. First, we install the necessary packages, prepare the environment, and download a small but capable model (Zephyr-7B):

pip install llama-cpp-python
CMAKE_ARGS="-DLLAMA_CUBLAS=on" FORCE_CMAKE=1 pip install llama-cpp-python
wget https://huggingface.co/TheBloke/zephyr-7B-alpha-GGUF/resolve/main/zephyr-7b-alpha.Q4_K_M.gguf

Loading a GGUF model with llama-cpp-python in BERTopic is straightforward:

from bertopic import BERTopic
from bertopic.representation import LlamaCPP

# Use llama.cpp to load in a 4-bit quantized version of Zephyr 7B Alpha
# and truncate each document to 50 words
representation_model = LlamaCPP(
    "zephyr-7b-alpha.Q4_K_M.gguf",
    tokenizer="whitespace",
    doc_length=50
)

# Create our BERTopic model
topic_model = BERTopic(representation_model=representation_model, verbose=True)

And that is it! We created a model that truncates input documents and creates interesting topic representations without being constrained by its token limit.

Thank you for reading!

If you are, like me, passionate about AI and/or Psychology, please feel free to add me on LinkedIn, follow me on Twitter, or subscribe to my Newsletter:

All images without a source credit were created by the author — Which means all of them, I like creating my own images ;)