9 Distance Measures in Data Science
Many algorithms, whether supervised or unsupervised, make use of distance measures. These measures, such as euclidean distance or cosine similarity, can often be found in algorithms such as k-NN, UMAP, HDBSCAN, etc.
Understanding the field of distance measures is more important than you might realize. Take k-NN for example, a technique often used for supervised learning. As a default, it often uses euclidean distance. By itself, a great distance measure.
However, what if your data is highly dimensional? Would euclidean distance then still work? Or what if your data consists of geospatial information? Perhaps haversine distance would then be a better alternative!
Knowing when to use which distance measure can help you go from a poor classifier to an accurate model.
In this article, we will go through many distance measures and explore how and when they best can be used. Most importantly, I will be talking about their disadvantages so that you can recognize when to steer clear of certain measures.
NOTE: For most distance measures long elaborate papers could and have been written on their use-cases, advantages, and disadvantages. I will try to cover as much as possible but may fall short! Thus, consider this article a global overview of these measures.
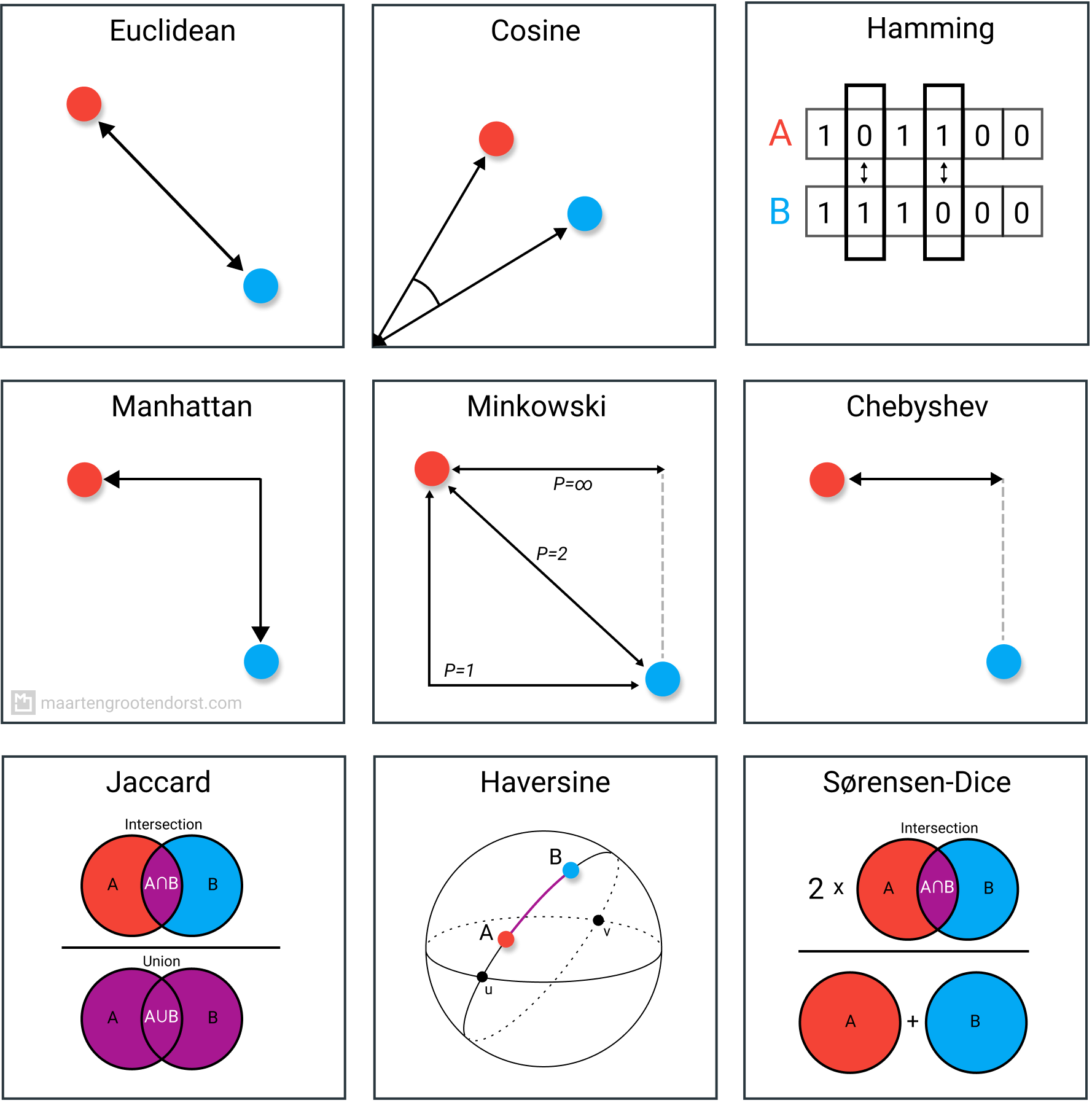
1. Euclidean Distance
We start with the most common distance measure, namely Euclidean distance. It is a distance measure that best can be explained as the length of a segment connecting two points.
The formula is rather straightforward as the distance is calculated from the cartesian coordinates of the points using the Pythagorean theorem.
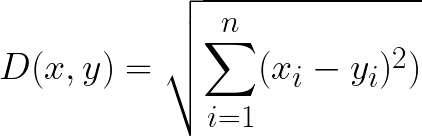
Disadvantages
Although it is a common distance measure, Euclidean distance is not scale in-variant which means that distances computed might be skewed depending on the units of the features. Typically, one needs to normalize the data before using this distance measure.
Moreover, as the dimensionality increases of your data, the less useful Euclidean distance becomes. This has to do with the curse of dimensionality which relates to the notion that higher-dimensional space does not act as we would, intuitively, expect from 2- or 3-dimensional space. For a good summary, see this post.
Use Cases
Euclidean distance works great when you have low-dimensional data and the magnitude of the vectors is important to be measured. Methods like kNN and HDBSCAN show great results out of the box if Euclidean distance is used on low-dimensional data.
Although many other measures have been developed to account for the disadvantages of Euclidean distance, it is still one of the most used distance measures for good reasons. It is incredibly intuitive to use, simple to implement and shows great results in many use-cases.
2. Cosine Similarity
Cosine similarity has often been used as a way to counteract Euclidean distance’s problem with high dimensionality. The cosine similarity is simply the cosine of the angle between two vectors. It also has the same inner product of the vectors if they were normalized to both have length one.
Two vectors with exactly the same orientation have a cosine similarity of 1, whereas two vectors diametrically opposed to each other have a similarity of -1. Note that their magnitude is not of importance as this is a measure of orientation.
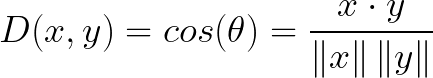
Disadvantages
One main disadvantage of cosine similarity is that the magnitude of vectors is not taken into account, merely their direction. In practice, this means that the differences in values are not fully taken into account. If you take a recommender system, for example, then the cosine similarity does not take into account the difference in rating scale between different users.
Use Cases
We use cosine similarity often when we have high-dimensional data and when the magnitude of the vectors is not of importance. For text analyses, this measure is quite frequently used when the data is represented by word counts. For example, when a word occurs more frequently in one document over another this does not necessarily mean that one document is more related to that word. It could be the case that documents have uneven lengths and the magnitude of the count is of less importance. Then, we can best be using cosine similarity which disregards magnitude.
3. Hamming Distance
Hamming distance is the number of values that are different between two vectors. It is typically used to compare two binary strings of equal length. It can also be used for strings to compare how similar they are to each other by calculating the number of characters that are different from each other.
Disadvantages
As you might expect, hamming distance is difficult to use when two vectors are not of equal length. You would want to compare same-length vectors with each other in order to understand which positions do not match.
Moreover, it does not take the actual value into account as long as they are different or equal. Therefore, it is not advised to use this distance measure when the magnitude is an important measure.
Use Cases
Typical use cases include error correction/detection when data is transmitted over computer networks. It can be used to determine the number of distorted bits in a binary word as a way to estimate error.
Moreover, you can also use Hamming distance to measure the distance between categorical variables.
4. Manhattan Distance
The Manhattan distance, often called Taxicab distance or City Block distance, calculates the distance between real-valued vectors. Imagine vectors that describe objects on a uniform grid such as a chessboard. Manhattan distance then refers to the distance between two vectors if they could only move right angles. There is no diagonal movement involved in calculating the distance.
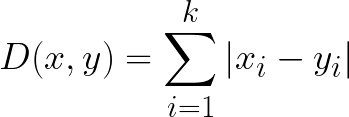
Disadvantages
Although Manhattan distance seems to work okay for high-dimensional data, it is a measure that is somewhat less intuitive than euclidean distance, especially when using in high-dimensional data.
Moreover, it is more likely to give a higher distance value than euclidean distance since it does not the shortest path possible. This does not necessarily give issues but is something you should take into account.
Use Cases
When your dataset has discrete and/or binary attributes, Manhattan seems to work quite well since it takes into account the paths that realistically could be taken within values of those attributes. Take Euclidean distance, for example, would create a straight line between two vectors when in reality this might not actually be possible.
5. Chebyshev Distance
Chebyshev distance is defined as the greatest of difference between two vectors along any coordinate dimension. In other words, it is simply the maximum distance along one axis. Due to its nature, it is often referred to as Chessboard distance since the minimum number of moves needed by a king to go from one square to another is equal to Chebyshev distance.
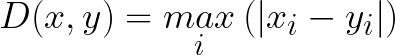
Disadvantages
Chebyshev is typically used in very specific use-cases, which makes it difficult to use as an all-purpose distance metric, like Euclidean distance or Cosine similarity. For that reason, it is suggested to only use it when you are absolutely sure it suits your use-case.
Use Cases
As mentioned before, Chebyshev distance can be used to extract the minimum number of moves needed by aking to go from one square to another. Moreover, it can be a useful measure in games that allow unrestricted 8-way movement.
In practice, Chebyshev distance is often used in warehouse logistics as it closely resembles the time an overhead crane takes to move an object.
6. Minkowski
Minkowski distance is a bit more intricate measure than most. It is a metric used in Normed vector space (n-dimensional real space), which means that it can be used in a space where distances can be represented as a vector that has a length.
This measure has three requirements:
-
Zero Vector— The zero vector has a length of zero whereas every other vector has a positive length. For example, if we travel from one place to another, then that distance is always positive. However, if we travel from one place to itself, then that distance is zero.
-
Scalar Factor— When you multiple the vector with a positive number its length is changed whilst keeping its direction. For example, if we go a certain distance in one direction and add the same distance, the direction does not change.
-
Triangle Inequality— The shortest distance between two points is a straight line.
The formula for the Minkowski distance is shown below:
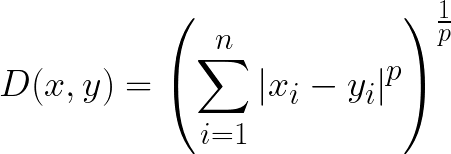
Most interestingly about this distance measure is the use of parameter p. We can use this parameter to manipulate the distance metrics to closely resemble others.
Common values of p are:
-
p=1 — Manhattan distance
-
p=2 — Euclidean distance
-
p=∞ — Chebyshev distance
Disadvantages
Minkowski has the same disadvantages as the distance measures they represent, so a good understanding of metrics like Manhattan, Euclidean, and Chebyshev distance is extremely important.
Moreover, the parameter p can actually be troublesome to work with as finding the right value can be quite computationally inefficient depending on your use-case.
Use Cases
The upside to p is the possibility to iterate over it and find the distance measure that works best for your use case. It allows you a huge amount of flexibility over your distance metric, which can be a huge benefit if you are closely familiar with p and many distance measures.
7. Jaccard Index
The Jaccard index (or Intersection over Union) is a metric used to calculate the similarity and diversity of sample sets. It is the size of the intersection divided by the size of the union of the sample sets.
In practice, it is the total number of similar entities between sets divided by the total number of entities. For example, if two sets have 1 entity in common and there are 5 different entities in total, then the Jaccard index would be 1/5 = 0.2.
To calculate the Jaccard distance we simply subtract the Jaccard index from 1:
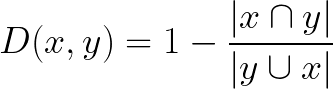
Disadvantages
A major disadvantage of the Jaccard index is that it is highly influenced by the size of the data. Large datasets can have a big impact on the index as it could significantly increase the union whilst keeping the intersection similar.
Use-Cases
The Jaccard index is often used in applications where binary or binarized data are used. When you have a deep learning model predicting segments of an image, for instance, a car, the Jaccard index can then be used to calculate how accurate that predicted segment given true labels.
Similarly, it can be used in text similarity analysis to measure how much word choice overlap there is between documents. Thus, it can be used to compare sets of patterns.
8. Haversine
Haversine distance is the distance between two points on a sphere given their longitudes and latitudes. It is very similar to Euclidean distance in that it calculates the shortest line between two points. The main difference is that no straight line is possible since the assumption here is that the two points are on a sphere.
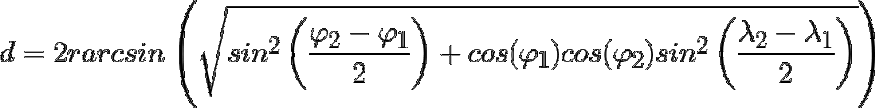
Disadvantages
One disadvantage of this distance measure is that it is assumed the points lie on a sphere. In practice, this is seldom the case as, for example, the earth is not perfectly round which could make calculation in certain cases difficult. Instead, it would be interesting to look towards Vincenty distance which assumes an ellipsoid instead.
Use Cases
As you might have expected, Haversine distance is often used in navigation. For example, you can use it to calculate the distance between two countries when flying between them. Note that it is much less suited if the distances by themselves are already not that large. The curvature will not have that large of an impact.
9. Sørensen-Dice Index
The Sørensen-Dice index is very similar to Jaccard index in that it measures the similarity and diversity of sample sets. Although they are calculated similarly the Sørensen-Dice index is a bit more intuitive because it can be seen as the percentage of overlap between two sets, which is a value between 0 and 1:
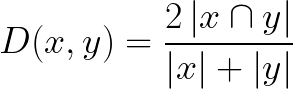
Disadvantages
Like the Jaccard index, they both overstate the importance of sets with little to no ground truth positive sets. As a result, it could dominate the average score taken over multiple sets. It weights each item inversely proportionally to the size of the relevant set rather than treating them equally.
Use Cases
The use cases are similar, if not the same, as Jaccard index. You will find it typically used in either image segmentation tasks or text similarity analyses.
NOTE: There are many more distance measures than the 9 mentioned here. If you are looking for more interesting metrics, I would suggest you look into one of the following: Mahalanobis, Canberra, Braycurtis, and KL-divergence.
Thank you for reading!
If you are, like me, passionate about AI, Data Science, or Psychology, please feel free to add me on LinkedIn or follow me on Twitter.








